[Log], [Entropy], [KL Divergence], [Cross Entropy]

探討Machine Learning中常用的KL Divergence，Cross Entropy, Maximum Likel意義

[Log]

• 
• 訊息量：通常會用log來描述某個機率隨機變數X發生x事件的訊息量。
  I(X=x) = -log( P(X=x) )
  I -> 訊息量
  P(X=x) -> 發生x事件的機率，介於0~1之間
  log -> 當輸入介於0~1之間，函數輸出 0 => -INF, 1 => 0
• 取負號-log使函數保有特性，機率越大的事件訊息量越小，反之則越大

[Entropy]

• 就是對訊息量求取的期望值，希望知道某機率隨機變數的不確定程度，數值越大，不確定信越高，訊息越多，所需要的編碼也會越多。又成”熵“
• H(X)=Ep[ -logp(x)] =−∑x∈Xp(x)logp(x) 
  
  The formula for entropy in the case of a two-valued variable is as follows:
  

  Entropy = -( p * log(p) + (1-p) * log(1-p) )
  舉例BOB考試有50%會及格，STEVE有90％會及格：
  H-BOB(X) = - ( 0.5 * log0.5 + (1 - 0.5) * log(1 - 0.5) ) = 0.3
  H-STEVE(X) = - ( 0.9 * log0.9 + (1 - 0.9) * log(1 - 0.9) ) = 0.14
  BOB 不確定性遠大於 STEVE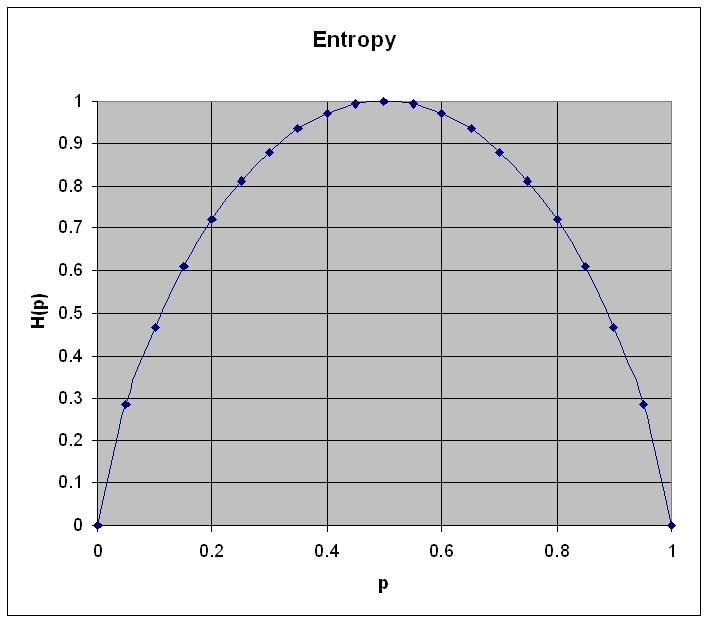
• 
  (以上的log皆為base-2 logarithm) -> (可以想成電腦bit的轉換）

[KL Divergence] (Kullback-Leibler) (Relative Entropy)

• 兩個隨機p(真實)和q(估計)機率分佈之間差距的度量！
• 記為DKL(p||q)，度量q分佈的無效性。
• DKL(p||q)=Ep[logp(x)q(x)]=∑x∈p(x)logp(x)q(x)  // Ep [log p(x) - log q(x)] 訊息量差的期望值
  =∑x∈[p(x)logp(x)−p(x)logq(x)]
  =∑x∈p(x)logp(x)−∑x∈p(x)logq(x) 
  =−H(p)−∑x∈p(x)logq(x) 
  =−H(p)+Ep[−logq(x)] 
  =Hp(q)−H(p) // 推倒成兩個分部的entorpy差距，不穩定性的相差，相對熵
• 確保連續性的假設：
  0log0
  
  0=0，0log0q=0，plogp0=∞ 
• if p==q, DKL(p||q)=0
• Hp(q)表示在p的機率分佈下，使用q分佈進行編碼的不穩定性，需要的bit編碼數量，H(p)表示真實需要的編碼數。
• KL Divergence其實很直覺的想法就是衡量估計的q來對p編碼和真實的p編碼兩者分佈的差異，以編碼數量的差，穩定性的差來表達。

[Cross Entropy]

• 交叉熵容易和相對熵搞混，兩者關係非常緊密，但有所區別。
• 定義如下：
  CEH(p,q)=Ep[−logq]=−∑x∈p(x)logq(x)=H(p)+DKL(p||q) 
• 從上面的相對熵解釋中就可以看出來，兩個根本就是差不多的東西，只是描述的目標不同。交叉善就是Hp(q) 前面已經解釋過了。
• 特别的，在logistic regression中， (B: Bernoulli distribution)
  p:真實樣本分佈，服從參數分佈為p的0-1分布，即X∼B(1,p) 
  q:估計出的分佈，服從參數分佈為q的0-1分布，即X∼B(1,q) 
• 兩者的交叉熵：CEH(p,q) 
  =−∑x∈p(x)logq(x) 
  =−[Pp(x=1)logPq(x=1)+Pp(x=0)logPq(x=0)] 
  =−[plogq+(1−p)log(1−q)] 
  =−[yloghθ(x)+(1−y)log(1−hθ(x))] 
  對所有訓練樣本取平均： 
  −1m∑i=1m[y(i)loghθ(x(i))+(1−y(i))log(1−hθ(x(i)))] 
  對這格結果與通過最大似然估計方法(Maximum Likelihood)求出的結果一致。

[Maximum Likelihood]

• 就是從現有的樣本(機率分佈q)中分析最接近真實(機率分佈p)的方法
• 應用：Generative Model就可以用Maximum Likelihood來表達學習現有的資料，來模擬真實資料的機率分佈，進而產生結果。
• <Maximum Likelihood>
  找出一組參數θ，可以讓 樣本機率分佈q 最大化近似 真實機率分佈p。相當於
  <KL Divergence>
  找出一組參數θ，可以 最小化 樣本機率分佈q 和 真實機率分佈p 所需編碼的差距最小。

Cross Entropy vs Mean Square Error

• 在分類時CE比MSE更適合，最直覺的想法就是分類網路最後的輸出會經過softmax，此時的數值會介於0~1之間，此時如果用MSE去計算loss，只會越來越小，最後導致gradient小到無法訓練。

REF:

• http://blog.csdn.net/rtygbwwwerr/article/details/50778098 
• https://en.wikipedia.org/wiki/Cross_entropy
• http://blog.xuite.net/metafun/life/69851478-%E8%B3%87%E8%A8%8A%E7%9A%84%E5%BA%A6%E9%87%8F-+Information+Entropy 
• https://jamesmccaffrey.wordpress.com/2013/11/05/why-you-should-use-cross-entropy-error-instead-of-classification-error-or-mean-squared-error-for-neural-network-classifier-training/